Horn bruges ofte i højttalersystemer af forskellige årsager. En kan være at give øget akustisk belastning til føreren, der er fastgjort til hornet. Dette er med til at øge følsomheden/effektiviteten. En anden kan være at give en vis kontrol over strålingsmønsteret for føreren, der er fastgjort til hornet. Det er dette direktivitetskontrolaspekt, som jeg vil fokusere opmærksomheden på i denne artikel.
I 1975 præsenterede Don Keele et papir på Audio Engineering Society's 51. konvent, der introducerede det moderne Constant Directivity-horn. Dette nye horndesign (nyt på det tidspunkt) kombinerede en eksponentiel halssektion for at give god belastning ved lavere frekvenser med en konisk eller lige vægsektion, der gav et mere ensartet dækningsmønster i det højere frekvensområde end et rent eksponentielt horn.
I dette papir bemærkede han forholdet mellem hornets dækningsvinkel, det lavfrekvente tab af retningsbestemmelseskontrol og hornmundingsstørrelsen, så ligning 1 er d = K/(Θ × fΘ).
Hvor:
d = hornets mundmål (enten vandret eller lodret)
Θ = dækningsvinklen for hornet (vandret eller lodret)
FΘ = lavfrekvent tab af retningsbestemt kontrol, Θ (vandret eller lodret) og K er en konstant med en empirisk udledt værdi eller 1 × 106″ × deg × Hz på 2,54 × 104m × grader × Hz.
Ud fra denne ligning kan du bestemme den hornmundingsdimension, der er nødvendig for at give retningsbestemmelseskontrol ned til en bestemt frekvens. For en fast dækningsvinkel kræves en større mundingsdimension for at opretholde denne dækning til en lavere frekvens. For hver oktav lavere, du ønsker retningskontrol (halvering af frekvens), skal munddimensionen fordobles.
Tilsvarende, hvis dækningsvinklen gøres mindre, skal hornmundingsdimensionen øges for at opretholde denne dækningsvinkel til en given frekvens. For hver halvering af dækningsvinklen skal mundmålet fordobles. Denne større mundstørrelse for en mindre dækningsvinkel virker modstridende for mange mennesker, når de først bliver præsenteret for den. Men på grund af disse irriterende fysiklove er det sådan, tingene fungerer. Det er ikke ulig de samme principper, der styrer opførselen af et linearray. At have den smalle lodrette dækningsvinkel, som de fleste af os forbinder med line arrays, til en lav frekvens kræver en lang line array.
Hvis du har et horn med en kendt dækningsvinkel, og du også kender munddimensionen, kan du omskrive denne ligning for at løse lavfrekvent tab af retningsstyring, hvilket giver ligning 2, fΘ = K/(Θ × d).
Over denne frekvens skal dækningsvinklen eller strålebredden være nogenlunde konstant. Under denne frekvens bør strålebredden dog stige, efterhånden som du mister styringen af retningsbestemmelsen. Dette er et ekstremt vigtigt punkt at huske på, når du vurderer potentielle højttalere til brug i systemdesign, hvor god retningsbestemmelse er påkrævet.
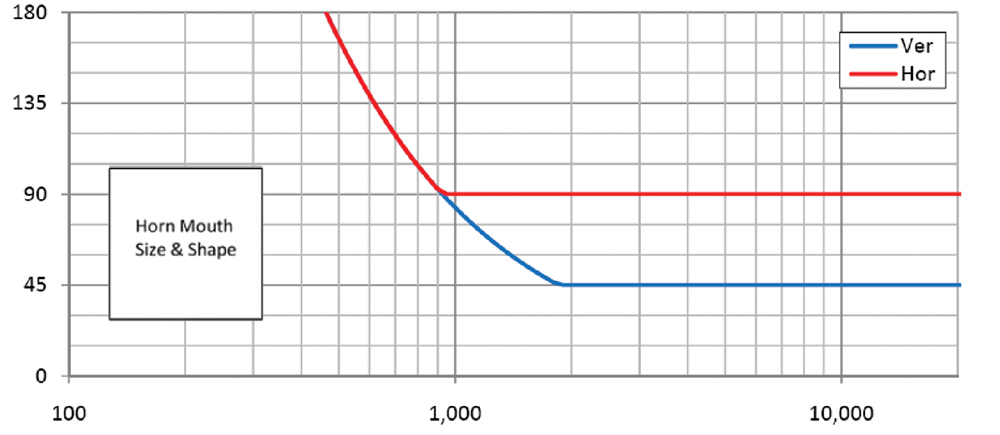
Figur 1: 12″ × 12″ firkantet mundhorn med 90° vandret og 45° lodret strålebredde.
Højttalerspecifikationsark refererer alt for ofte til et nominelt dækningsmønster med ringe kvalifikation med hensyn til det frekvensområde, over hvilket denne strålebredde faktisk opretholdes. Som du vil se senere, kan udeladelse af disse oplysninger og en fejlagtig antagelse fra designerens side give mindre end de ønskede slutresultater.
For at bestemme dækningen af et horn under den frekvens, ved hvilken det begynder at miste retningskontrol, kan du igen omskrive ligning 1 ved at løse dækningsvinklen for at få ligning 3, Θ = K/(d × f). Bemærk, at jeg har erstattet en hvilken som helst frekvens, f, for lavfrekvent tab af retningsstyring, fΘ. Dette er gyldigt, så længe du begrænser det til frekvenser, der er lavere end lavfrekvent tab af retningsbestemt kontrol. Ved højere frekvenser end dette, bør strålebredden være relativt konstant ved designdækningsvinklen.
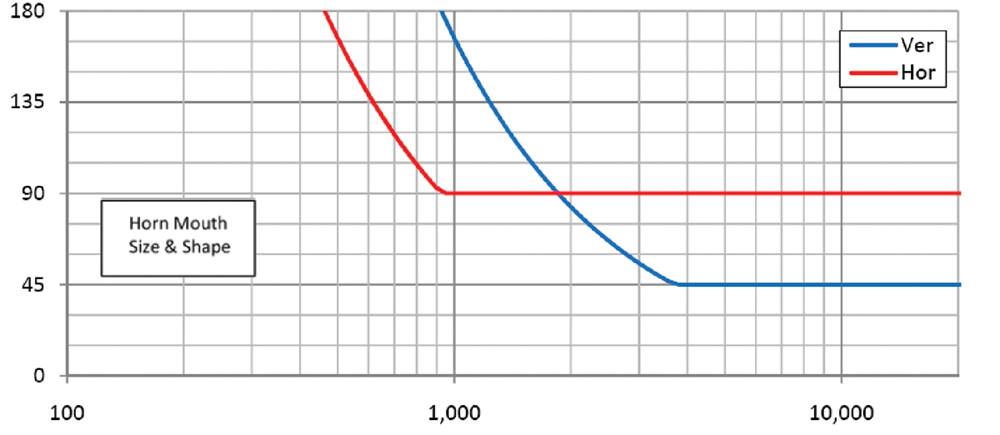
Tegning af ligning 3 vil indikere, hvordan tabet af retningsbestemt kontrol skrider frem med faldende frekvens. Dette er vist i fig. 1 for et hypotetisk horn med vandrette og lodrette dækningsvinkler på henholdsvis 90° og 45°.
Hornet har en 12" (30 cm) firkantet mund. Et rigtigt horn opfører sig måske ikke helt så godt i området omkring det indledende tab af retningskontrolfrekvens. Dette er med vilje ikke vist, fordi dets årsag ligger uden for denne artikels omfang og for at forenkle præsentationen af det relevante emne.
Som du kan se på grafen, begynder den vandrette strålebredde på 90° at stige lige over 900Hz. Den lodrette strålebredde på 45° begynder at stige ved ca. 1,8 kHz. Med henvisning tilbage til ligning 2 kan du se, hvorfor dette sker. Den lodrette strålebredde er halvdelen af værdien af den vandrette strålebredde. Hornmundingen er 12" (30 cm) i både det vandrette og lodrette plan, og d er konstant.
Således er det vertikale tab af retningsbestemt kontrolfrekvens, fΘV, det dobbelte af det horisontale tab af direktivitetsstyringsfrekvens, fΘH.
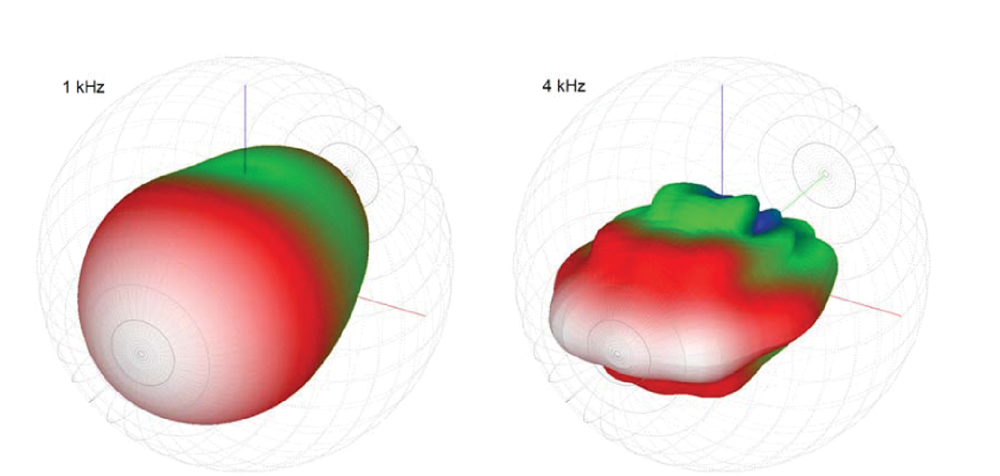
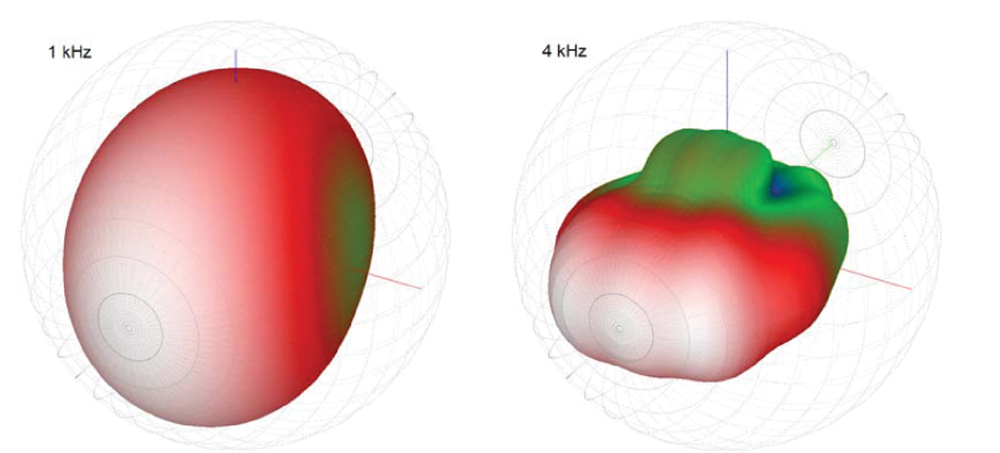
Figur 2: Retningsballoner til 12″ × 12″ kvadratisk mundhorn.
Dette er også illustreret i retningsbestemt balloner vist i fig. 2. Ved 4kHz er 90° × 45° dækningsmønsteret godt opretholdt. Ved 1 kHz kan tabet af lodret retningsstyring forstås, da dækningsmønsteret virker næsten aksesymmetrisk. Denne adfærd antydes også af strålebreddegraferne i fig. 1. Ved 1 kHz er den vandrette og lodrette strålebredde begge ca. 90°.
Generelt vil firkantede mundhorn have et forhold mellem frekvenserne for vandret og lodret tab af retningsbestemt kontrol, der er det samme som forholdet mellem den lodrette og vandrette dækningsvinkel. For mit eksempel på 90° og 45° er dette præcis tilfældet, da forholdet er 2:1. Hvis hornet, med den samme 12″ kvadratiske mund, havde en lodret strålebredde på 60°, ville du forvente, at forholdet var 3:2 for 90° × 60° hornet.
Dette ville placere det vertikale tab af retningsbestemt kontrolfrekvens på en smule over 1,35 kHz. For at tabet af retningsbestemt kontrolfrekvenser skal være det samme for både den vandrette og lodrette strålebredde, skal den mere snævre dækningsvinkel have en mundingsdimension, der er større med forholdet mellem dækningsvinklerne. Lad os sige, at du vil ændre eksempelhornet for at dette kan ske. Dækningsvinkelforholdet på 2:1 ville betyde, at den lodrette mundingsdimension, højden, skulle være dobbelt så stor som den vandrette mundingsdimension, bredden. Så du ville nu have en hornmund, der er 12" (30 cm) bred og 24" (61 cm) høj.
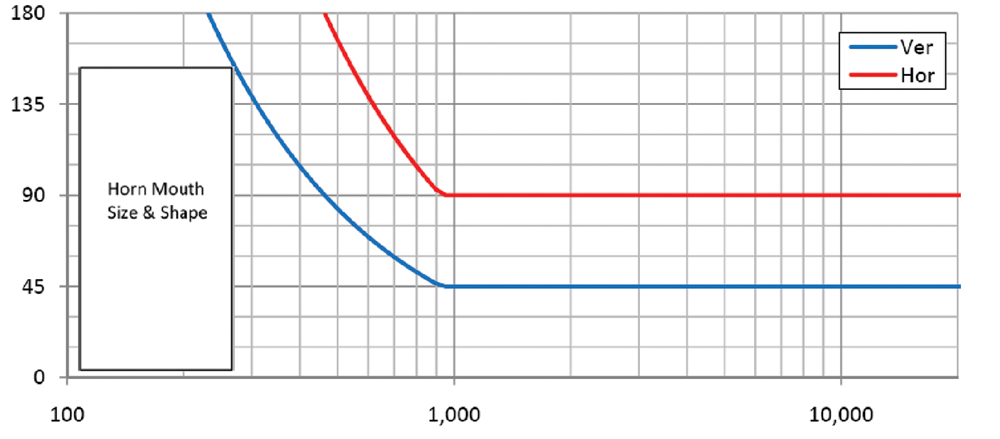Figur 3: 12″ × 24″ mundhorn med 90° vandret og 45° lodret strålebredde.
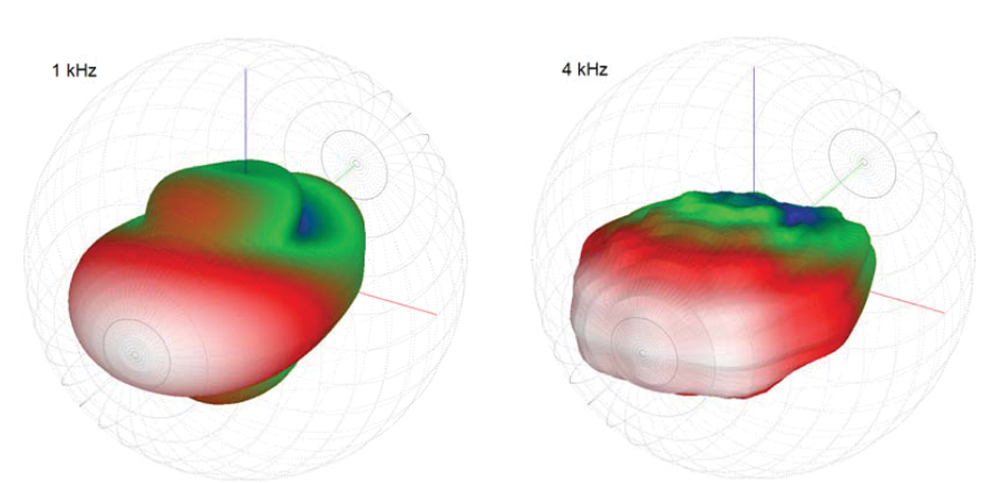
Figur 4: Retningsballoner til 12″ × 24″ mundhorn.
Dette kan verificeres ved at bruge ligning 1 til at beregne den nye nødvendige højdedimension. Med denne nye højde kan ligning 3 igen bruges til at tegne strålebredden (fig. 3). Retningsballonerne til dette 24" høje horn (fig. 4) viser den forbedrede retningsbestemmelseskontrol ved 1kHz sammenlignet med det 12" høje horn (fig. 2).
Hvad med et mere almindeligt set horn, et med en højde, der er meget mindre end bredden? For 90° × 45° horn fra nogle producenter ville mundmål på 12″ (30cm) × 6″ (15cm) ikke være ud over det sædvanlige. Igen vil jeg bruge ligning 2 til at beregne den nye frekvens for det vertikale tab af retningsvirkningskontrol med det mere almindeligt dimensionerede horn. Dette viser sig at være 3,7 kHz. Brug af ligning 3 til at tegne en graf for strålebreddeudbyttet Fig. 5.
Her ser du noget meget interessant, der ikke er til stede i de foregående grafer. Under 2kHz er den lodrette strålebredde faktisk større end den vandrette strålebredde! Dette omtales nogle gange som "mønsterflip". Det lodrette dækningsmønster af hornet, som formodes at være smallere end det vandrette dækningsmønster, er nu den bredere dækningsvinkel. Med andre ord er den vandrette og lodrette strålebredde vendt i forhold til, hvilken der er størst og hvilken der er mindre. Dette er især bemærkelsesværdigt, når man undersøger retningsbestemt balloner vist i fig. 6.
Figur 5: 12″ × 6″ mundhorn med 90° vandret og 45° lodret strålebredde.
Som nævnt tidligere, hvis specifikationsarket for en højttaler, der anvender et horn med lignende dimensioner, blot gav de tilsigtede eller nominelle dækningsvinkler med ringe eller ingen information om det frekvensområde, over hvilket dækningsvinklerne blev opretholdt, kan du fejlagtigt tro, at den angivne strålebredde gælder for et meget større frekvensområde, end det faktisk er muligt. Som sådan er højttalerydelsen vist i fig. 5 og 6 fungerer muligvis ikke godt til applikationer, der kræver god retningskontrol for at lette tilstrækkelig taleforståelighed.
Den tilsigtede lodrette strålebredde på 45° opnås kun over 3,7 kHz. Under denne frekvens kan der sættes en del akustisk energi ind i områder, hvor det ikke er ønsket. Dette vil blive mærkbart, når du kortlægger dækningen af en højttaler ved hjælp af en af disse typer horn i et rum. Det andet punkt, der kan observeres, er, at under 2kHz kan højttaleren fungere bedre, hvis den blev vendt på siden. Dette ses også på fig. 6.
Som med de fleste ingeniørøvelser er der flere punkter, der skal afbalanceres, når det kommer til horns retningsbestemte ydeevne: smal dækningsvinkel, den ønskede lave frekvens for at opretholde dækningsvinklen og lille hornstørrelse; vælg to. De to, du vælger, vil diktere, hvad den tredje skal være. Du kan ikke vilkårligt have alle tre på samme tid.
Jeg håber, at dette har været med til at forklare lidt om, hvordan et horns frekvensafhængige retningsvirkning hænger sammen med dets størrelse. Små horn kan simpelthen ikke give små dækningsvinkler ved lave frekvenser. Pas på dem, der forsøger at rådgive anderledes.
Figur 6: Retningsballoner til 12″ × 6″ mundhorn.
Denne artikel blev oprindeligt publiceret i Voice Coil, november 2010.